Ansys Additive Suite
Komplexní řešení pro designery aditivní výroby
Nástroj pro simulaci procesu 3D tisku a tepelného zpracování
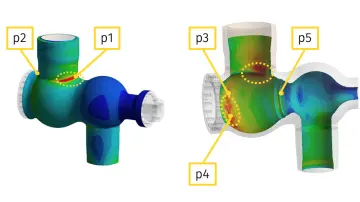
Ansys Additive Suite je vhodný také pro predikci zbytkových napětí a deformací po výtisku či pro optimalizaci tisku.


Příklady využití v praxi
- Vytváření podpor a build souborů pro různé typy tiskáren
- Optimalizace rozmístění podpor
- Lokalizace problematických míst (s vysokými zbytkovými napětími, velkými deformacemi, přehříváním, …)
- Kompenzace deformací vytištěné součásti
- Simulace tepelného zpracování vytištěné součásti
Klíčové vlastnosti
- Simulace PBF, DED, Metal Sintering metod tisku
- Predikce deformací a zbytkových napětí
- Kompenzace deformací
- Možnost vytváření vlastních modelů materiálu
Bonusy:
- Předdefinované modely materiálu pro 17-4PH Stainless Steel, 316 Stainless Steel, AlSi10Mg, Inconel 625, Inconel 718 a Ti-6Al-4V


Soubory ke stažení
Document
Učte se s námi online!
Oceňované bezplatné semináře pro podporu výuky a pro zdokonalování se v práci se software Ansys